Optimization of entropy calculations

The information-theoretical quantity known as the O-information (short for "information about Organisational structure") is used to characterise statistical interdependencies within multiplets of three and more variables. It enables us to determine the nature of the information, i.e. whether multiplets are primarily carrying redundant or synergistic information, in addition to quantifying how much information multiplets of brain areas are carrying. It takes an extensive amount of computation to estimate HOIs. The O-information is a perfect choice to estimate HOIs in a timely manner because its computational cost just requires basic quantities like entropies. There is yet no neuroinformatic standard of merit for HOI estimation that can be used by aficionados of all skill levels in a reasonable amount of time.
Published on June 21, 2023 by Dishie Vinchhi
sample post test
Introduction to task
In the world of data analysis and machine learning, efficiency is often a key concern. The HOI (Higher Order Information) repository, a powerful tool for studying information dynamics, presents an interesting case study in optimizing computation processes. By default, the ent_g function inside the HOI repo computed the entropy (required to calculate o-information) over the two last axes (n_variables, n_features, n_samples). This approach was used to avoid loops. This task is to use jax.vmap() in the implementation and compare the two approaches for computation times.
Criteria to keep in mind
Ensuring Result Consistency The first step in this analysis involves validating the accuracy of the “map” approach against the traditional tensor approach. It’s crucial to verify that the new implementation produces the same results as the original one, thereby ensuring data integrity and the preservation of meaningful information.
Comparing Computation Time Efficiency is a cornerstone of effective computation. By measuring and comparing the computation times of both the traditional tensor approach and the proposed map approach, we can ascertain whether the latter offers significant time savings. This comparison will provide valuable insights into which approach is more suitable for practical implementation.
Assessing GPU Memory Consumption Memory utilization is a critical consideration, especially when dealing with large datasets or resource-intensive computations. By evaluating the GPU memory required by each approach, we can determine if the map approach exhibits any advantages or disadvantages in terms of memory efficiency.
About jax.vmap()
vmap is a feature in JAX that enables efficient parallelization of functions over arrays or sequences of inputs.
- vmap stands for “vectorized map” and is a powerful feature that enables efficient parallelization of functions over arrays or sequences of inputs.
- With vmap, we can apply a function to a batch of inputs, eliminating the need for explicit looping. This not only simplifies the code but also significantly improves performance, especially when dealing with large datasets or complex computations.
Original code (Tensor implementation)
The following piece of code computes the entropy on a multidimensional array over the two last axes :
@partial(jax.jit, static_argnums=1)
def ent_tensor(x: jnp.array, biascorrect: bool=True) -> jnp.array:
"""Entropy of a tensor of shape (..., n_features, n_samples)"""
nvarx, ntrl = x.shape[-2], x.shape[-1]
# demean data
# x = x - x.mean(axis=1, keepdims=True)
# covariance
c = jnp.einsum('...ij, ...kj->...ik', x, x)
c /= float(ntrl - 1.)
chc = jnp.linalg.cholesky(c)
# entropy in nats
hx = jnp.log(jnp.einsum('...ii->...i', chc)).sum(-1) + 0.5 * nvarx * (
jnp.log(2 * jnp.pi) + 1.0)
ln2 = jnp.log(2)
if biascorrect:
psiterms = psi((ntrl - jnp.arange(1, nvarx + 1).astype(
float)) / 2.) / 2.
dterm = (ln2 - jnp.log(ntrl - 1.)) / 2.
hx = hx - nvarx * dterm - psiterms.sum()
return hx / ln2
Vmap implementation
The following piece of code computes the entropy on a two dimensional array and the
jax.vmapgeneralizes the computations to a 3D array :
@partial(jax.jit, static_argnums=1)
def ent_vector(x: jnp.array, biascorrect: bool=True) -> jnp.array:
"""Entropy of an array of shape (n_features, n_samples)."""
nvarx, ntrl = x.shape
# demean data
# x = x - x.mean(axis=1, keepdims=True)
# covariance
c = jnp.dot(x, x.T) / float(ntrl - 1)
chc = jnp.linalg.cholesky(c)
# entropy in nats
hx = jnp.sum(jnp.log(jnp.diagonal(chc))) + .5 * nvarx * (
jnp.log(2 * jnp.pi) + 1.)
ln2 = jnp.log(2)
if biascorrect:
psiterms = psi((ntrl - jnp.arange(1, nvarx + 1).astype(
float)) / 2.) / 2.
dterm = (ln2 - jnp.log(ntrl - 1.)) / 2.
hx = hx - nvarx * dterm - psiterms.sum()
# convert to bits
return hx / ln2
ent_vector_vmap= jax.vmap(ent_vector)
Following is the comparison in computation times between tensor and vmap implementation
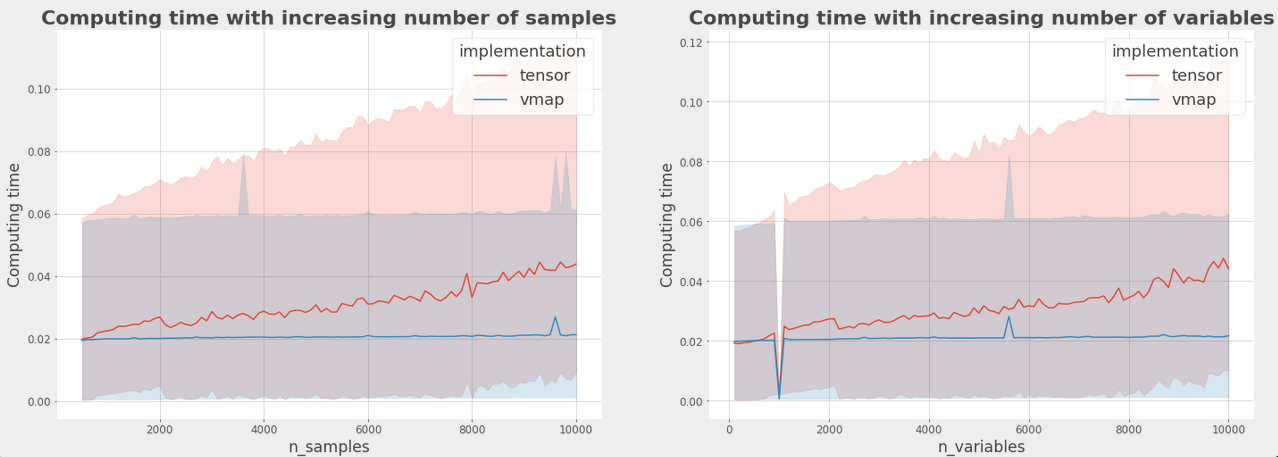
- Here the blue line represents the computation time for the vmapped implementation while the red line represents the tensor version.
- The first graph has varying number of n_samples on the x axis and the second graph has n_variables as the changing parameters.
- The constant time taken for computation by the vammped implementation even with a large increase i size of input data is a result of its ust-In-Time (JIT) compilation and parallel computing.